Symplectic vector field

In physics and mathematics, a symplectic vector field is one whose flow preserves a symplectic form. That is, if 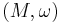$(M,\omega)$ is a symplectic manifold, then a vector field 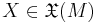$X\in\mathfrak{X}(M)$ is symplectic if its flow preserves the symplectic structure. In other words, the Lie derivative must vanish:

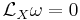$\mathcal{L}_X\omega=0$ .^[1]

Alternatively, a vector field is symplectic if its interior product with the symplectic form is closed.^[1] (The interior product gives a map from vector fields to 1-forms, which is an isomorphism due to the nondegeneracy of a symplectic form.) The equivalence of the definitions follows from the closedness of the symplectic form and Cartan's magic formula for the Lie derivative in terms of the exterior derivative.

If the interior product of a vector field with the symplectic form is exact (and in particular, closed), it is called a Hamiltonian vector field. If the first De Rham cohomology group 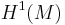$H^1(M)$ is trivial, all closed forms are exact, so all symplectic vector fields are Hamiltonian. That is, the obstruction to a symplectic vector field being Hamiltonian lives in 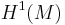$H^1(M)$ . In particular, symplectic vector fields on simply connected spaces are Hamiltonian.

The lie bracket of two symplectic vector fields is Hamiltonian, and thus the collection of symplectic vector fields and the collection of Hamiltonian vector fields both form lie algebras.

References

^ ^a ^b Cannas da Silva, Ana (2001), Lectures on Symplectic Geometry, Lecture Notes in Mathematics, 1764, Springer-Verlag, p. 106, ISBN 9783540421955 .

This article incorporates material from Symplectic vector field on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.